凸包 Gift wrapping 算法(2D)

开始干正事了。。。最近整理一个四面体剖分的串讲，准备从 2D 的 Delaunay 三角剖分开始讲, 索性就把凸包也顺便介绍一下吧。

这篇开个头，讲讲凸包的经典算法系列，计划一篇一个算法。

所谓凸包，就是给定二维平面上的点集，将最外层的点连接起来构成的凸多边型，严谨的定义咱就不说了，如下图（图都是从维基百科上偷来的 (>.<) ）：

convex hull

凸包算法已经十分成熟，有名的算法有 Gift wrapping, Graham scan, QuickHull, Divide and conquer, Monotone chain, Incremental convex hull algorithm, The ultimate planar convex hull algorithm, Chan’s algorithm 等。

本篇介绍第一个算法： Gift wrapping 。这个算法是凸包算法里面最简单的算法之一，1970 年就被提出来了。又叫做 Jarvis march 算法。

不知道大家第一次听到凸包会想怎么去求，我第一印象就是平面上钉了有一堆钉子（点集），然后我们用线拴住最外面任意一个，拉紧绳子沿着外延绕一圈，就可以得到这堆钉子的凸包。

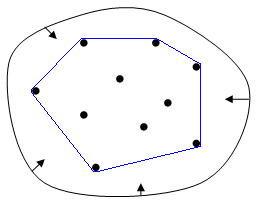
OK，原理介绍完了。。。看图：

gift wrapping

如上图：

首先我们选择一个一定在凸包上的点，这个点最简单的就是找最上，最下，最左或最右的点，上图使用了最左边的点;
假如挑最左边的点，所有点都在选定点的右边，用一条竖直的射线向右扫描，可以找到第二个点;
取最近找到的两个点，比如 $p_0$，$p_1$，所有点一定在他们连线的右边，用连线所在直线沿 $p_1$ 向右扫描，可以找到下一个点;
直到找到起始点，凸包就找到了。

不难发现，扫描过程其实是遍历所有的点，求向量夹角得到的，取上图中 $p_0$，$p_1$ 为例子，$\vec{p_0 p_1}$ 为起始方向，我们要找一个 $p_2$ 使得 $\vec{p_0 p_1}$ 和 $\vec{p_1 p_2}$ 的夹角最小，这样我们就找到了最边上的点。

如果总共有 $n$ 个点，最后的凸包上有 $h$ 个点，由于每个凸包上点都需要遍历所有的点，该算法的时间复杂度为 $O(nh)$，最坏的情况是 $O(n^2)$，此时所有点都在凸包上。所以如果凸包上的点数量很少时，这个算法还是很快的。

实现如下

/**
* gift_wrapping algorithm to calculate convex hull
*/
std::vector<Point> gift_wrapping(const std::vector<Point>& pts)
{
    std::vector<Point> hull;

    // too little points, the original set is a "cenvex hull"
    if (pts.size() <= 3) {
        hull.insert(hull.begin(), pts.begin(), pts.end());
        return hull;
    }

    // find the first point on the convex hull, here I use the leftmost one
    static const REAL MAX_REAL = std::numeric_limits<REAL>::max();
    Point leftmost(MAX_REAL, MAX_REAL);
    for (unsigned long i = 0; i < pts.size(); ++i) {
        if (leftmost.x > pts[i].x) {
            leftmost = pts[i];
        }
    }
    hull.push_back(leftmost);

    // p0, p1, p2
    Point p0(leftmost.x, leftmost.y - 1),
        p1 = leftmost,
        p2,
        p_cur;
    Vector vec_left, vec_right;
    REAL max_cos = -1.1, cur_cos;

    while (true) {
        max_cos = -1.1;
        vec_left.set(p0, p1);
        for (unsigned long i = 0; i < pts.size(); ++i) {
            p_cur = pts[i];
            if (p_cur == p1) {
                continue;
            }

            vec_right.set(p1, p_cur);
            cur_cos = Vector::cosAngle(vec_left, vec_right);
            if ((cur_cos > max_cos) || (cur_cos == max_cos &&
                        ((std::fabs(vec_right.x) > (std::fabs(p2.x - p1.x))) ||
                        (std::fabs(vec_right.y) > (std::fabs(p2.y - p1.y)))))) {
                max_cos = cur_cos;
                p2 = p_cur;
            }
        }

        // convex hull found
        if (p2 == hull[0]) {
            break;
        }

        hull.push_back(p2);

        // to find next
        p0 = p1;
        p1 = p2;
    }

    return hull;
}

这个算法可以推广到更高维，等下次再贴一个 3D 的实现上来。